4 basic sorting algorithms everyone must know
In this article let's learn what is sorting algorithm is and the different types of sorting algorithms
Topics covered:
- Sorting algorithms
- Different types of sorting algorithms
- Use cases of different sorting algorithms
Sorting algorithms
A sorting algorithm is used to arrange elements of an array/list in a specific order( either ascending or descending order)

4 basic sorting algorithms can be used to complete this operation. And, we can use any algorithm based on the requirement.
4 Basic Sorting Algorithms
- Bubble Sort
- Selection Sort
- Insertion Sort
- Cyclic Sort
Bubble Sort:
Like the air bubbles rising to the surface, the largest elements in the array move to the end part of the array after every iteration. In bubble sort, the algorithm compares two adjacent elements and swaps them till the elements are in their specific order.
Working of Bubble Sort
Let us take the above example and sort the elements in ascending order.
- Always start a comparison between elements from the index one irrespective of iteration.
- If the first element is greater than the second element then swap and continues the comparison.

- Here after 1st iteration the largest element is sorted or placed in its largest index.

- "i" value = iteration number = the number of times outer loop runs.
- We notice that in the second iteration after 4 (element) was placed in index 3, we didn't compare element 4 and element 5 because we already know that the elements are being placed in their respective positions. Hence, it's waste of comparing 4 with 5.
- "j" value is for comparison. if arr[j] < arr[j-1] , then swap.
as it is not required to compare with already sorted elements, j < arr.length-i.
At the end, if there is no swapping then the array is sorted.
Code:
static void bubble( int[] arr){
// run the iterations in (arr.length - 1) times
for(int i = 0; i < arr.length; i++){
// for each iteration, maximum item is placed in it's respective index
boolean swapped = false;
for(int j = 1; j < arr.length - i; j++){
// Swap if the element is smaller than prev one
if( arr[j] < arr[j-1]){
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
swapped = true;
}
}
if(!swapped){ // if no swap then elements are sorted
break}
}
}
- As the size of the array is growing, the number of comparisons are also growing.
Complexities:
Worst case Time complexity: If the array is in ascending order but we need to sort it in descending order then it's the worst case. The time complexity is O(n*2). Best case Time complexity: O(n)
Space complexity: O(1)
Bubble sort is a stable sorting algorithm.
Advantages of Bubble sort:
- The built-in ability to detect whether the list is sorted efficiently or not.
- Bubble sort can be implemented recursively.
Disadvantages:
- It is effective only if the size of the array is small, for larger samples the number of comparisons increases.
Selection sort:
Select the larger element and put it in its respective larger index by swapping the elements.
- First find the max element
- Swap the max element with its respective max index element
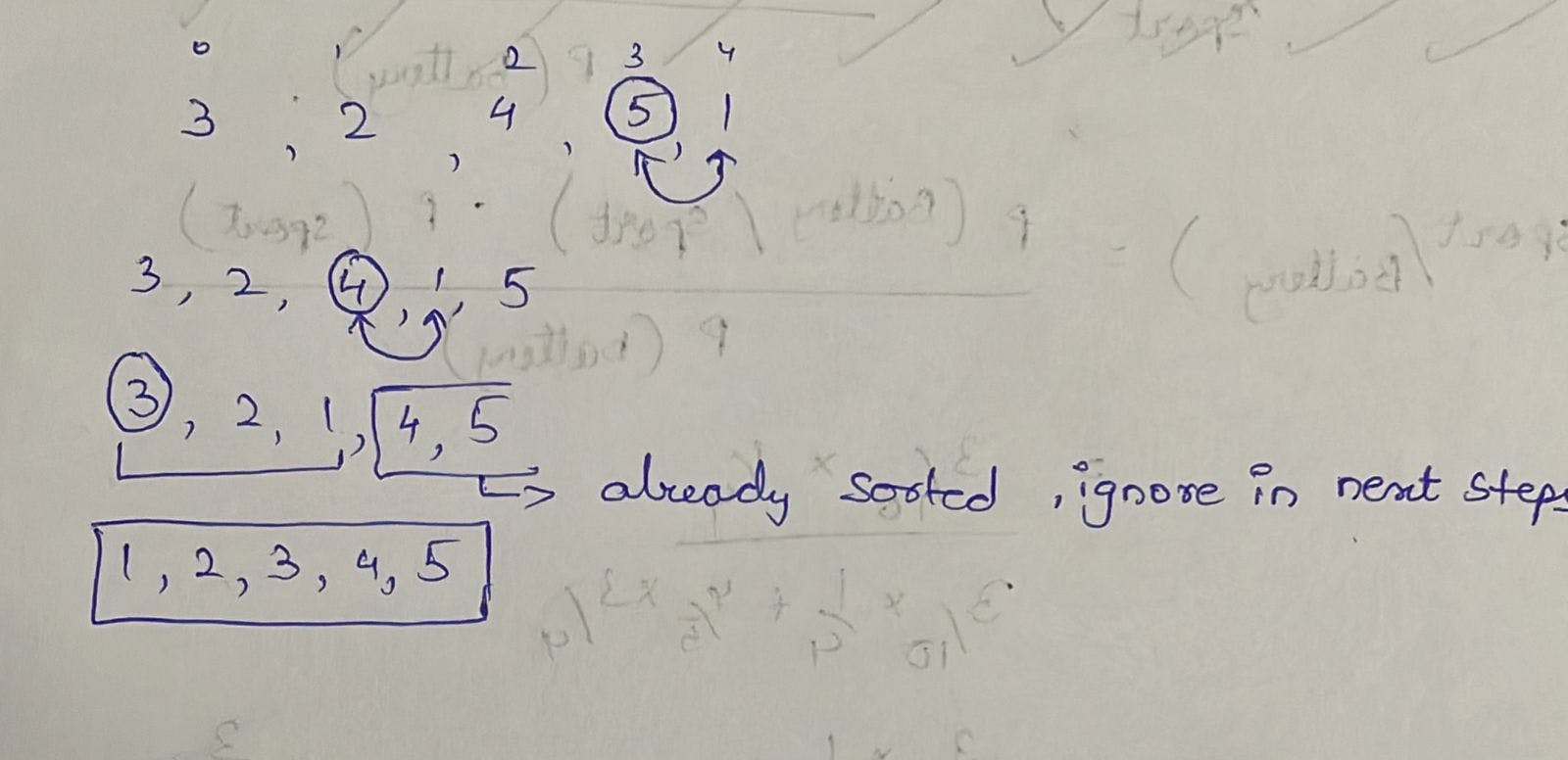
Code:
static void selection(int[] arr){
for(int i = 0; i < arr.length; i++){
// find max element in remaining array and swap
int last = arr.length - i - 1; // last elements which are already sorted are ignore.
int maxInd = getMaxInd(arr, start, last);
swap(arr, maxInd, last);
}
}
static int getMaxInd(int[] arr, int start, int end){
int max = start;
for(int i = start; i <= end; i++){
if(arr[max] < arr[i]){
max = i;}
}
return max;
}
static void swap(int[] arr, int first, int second){
int temp = arr[first];
arr[first] = arr[second];
arr[second] = temp;
}
Complexity:
Best case: O(N2) Worst case: O(N2) In both cases, the time complexity is the same, because in any case, it's finding the maximum element.
Use case:
- Performs well on a small list.
- Cost of swapping does not matter
- Checking all the elements is compulsory
- Cost of writing to memory matters like in flash memory (number of writes/swaps is O(n) as compared to O(n2) of bubble sort)
Disadvantage:
It is not a stable algorithm
Insertion Sort:
Sorting the given sample in parts by parts. For every index, put that index element at the correct index on Left Hand Side.

- When i = 0 and j = 1, it means sort the array till index 1, similarly i = 1 and j = 2 means sort the array till index 2.
- i <= N-2 , because j is always i + 1, if i exceeds N - 2 then j value becomes index out of bound.
- At any point of time if j is not smaller than prev element then no need to check other left hand side element because the left part is already sorted. So break the loop.
Use case:
- Adaptive: Steps get reduced if array is sorted. Number of swaps reduces as compared to bubble sort.
- It is a stable sorting algorithm
- Used for smaller values of N.
- Works good when the array is partially sorted. That's why it is mainly helpful in hybrid sorting algorithms.
static void insert(int[] arr){
for(int i = 0; i < arr.length - 1; i++){
for(int j = i+1; j > 0; j--){
if(arr[j] < arr[j-1]){
swap(arr, j , j - 1)
}else{
break;
}
}
}
}
Cyclic Sort:
When the given numbers are from range 1 to N, then use cyclic sort
In the sorted array,
every element index value is (element value - 1) because the index in the array starts from 0.
Every unique item is getting swapped once.
The best algorithm because it sorts the array in a single pass.
static void sort(int[] arr){
int i = 0;
while(i < arr.length){
int correct = arr[i] - 1;
if( arr[i]!= arr[correct] ){
swap(arr, i , correct);
} else{i++}
}
}
}
Complexity: Time complexity is O(N*2).
